Det er en økende interesse for å ta i bruk omvendt undervisning («flipped classroom») som undervisningsmetode. Mange elever opplever matematikkfaget som spesielt utfordrende, og det er viktig å finne måter å møte disse elevene og deres faglige utfordringer på. Denne systematiske kunnskapsoppsummeringen undersøker bruk av omvendt undervisning i matematikkfaget, og med utgangspunkt i funnene presenterer forfatterne 10 prinsipper til støtte i implementering av omvendt undervisning i matematikk.
Et forskningsnotat er en forenklet og forkortet oppsummering av publiserte systematiske kunnskapsoversikter. Forskningsnotatet gjør forskningen mer tilgjengelig og leservennlig.
Fordelene ved omvendt undervisning i matematikk berører elevene direkte, i og med at disse fordelene inkluderer flere tilbakemeldinger fra lærer, flere muligheter til samarbeid, samt mer tid til å utforske og forstå vanskelige matematiske konsepter og tematikker.
Bakgrunn
Matematikk spiller en viktig rolle både i individets og samfunnets utvikling. Mange elever utrykker at de synes matematikk er et stressende og vanskelig fag, og på lang sikt kan negative erfaringer med matematikkfaget forhindre at elever velger realfag i høyere utdanning. For bedre å ivareta elevenes behov og for å skape engasjement rundt matematikk har flere matematikklærere foreslått bruk av omvendt undervisning i matematikklasserommet.
Tradisjonell undervisning er undervisning hvor majoriteten av undervisningen i klasserommet består av lærerstyrt tavleundervisning, mens lekser, gruppearbeid og forberedelse til elevpresentasjoner i hovedsak skjer utenfor klasserommet. Omvendt undervisning handler om å sette av mer tid til elevaktivitet i klasserommet ved å flytte tavleundervisningen over på en annen plattform i forkant av skoletimen. I stedet for å bruke tid på at læreren gjennomgår teori i klasserommet, forbereder elevene seg til timen ved bruk av videoer eller andre ressurser som for eksempel digitale spill eller podkaster. Arbeid med disse ressursene blir elevenes hjemmelekse og kommer i stedet for å gjøre oppgaver som repeterer teori fra forrige skoletime. Rekkefølgen på undervisning på den ene side og elevenes arbeid med det som det har blitt undervist i på den andre, blir dermed snudd, og vi får omvendt undervisning. Ved hjelp av ressurser som videoopptak som eleven ser i leksetiden hjemme, får eleven anledning til å lære i sitt eget tempo, blant annet fordi eleven kan sette videoen på pause og spole frem og tilbake. Når elevene kommer til klasserommet, har læreren mer tid til å legge opp til elevaktiv læring, for eksempel diskusjoner, problemløsing og samarbeid. Dessuten får lærer mer tid til å vurdere og veilede elevene individuelt i deres læring.
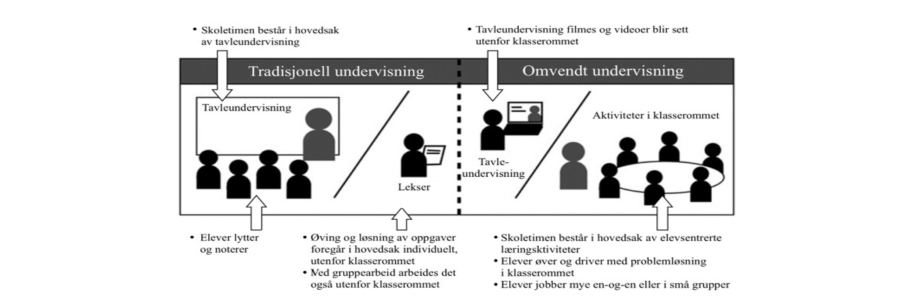
En økende interesse for denne undervisningsmetoden er bakgrunnen for forfatternes ønske om å undersøke hvordan omvendt undervisning faktisk fungerer i praksis for matematikkfaget.
Formål
Gjennom en meta-syntese analyseres tidsskriftsartikler om omvendt undervisning i matematikk. Fokuset ligger på de følgende fire spørsmålene:
- Hvilke undervisningsmetoder brukes i og utenfor klasserommet ved omvendt undervisning i matematikk?
- Hvilken effekt har omvendt undervisning på elevenes prestasjoner i matematikkfaget sammenlignet med mer tradisjonelle former for undervisning?
- Hvordan drar elever og lærere nytte av omvendt undervisning i matematikk?
- Hva er utfordringene med implementering av omvendt undervisning i matematikk?
Med utgangspunkt i disse spørsmålene presenterer forfatterne 10 prinsipper for gjennomføring av omvendt undervisning i matematikk.
Inkluderte studier
Metasyntetiseringen ble foretatt på bakgrunn av 61 studier fra perioden 2012–2016. Artikkelforfatterne brukte ikke geografiske restriksjoner, så studiene kommer fra en rekke land som USA, Taiwan, Canada, Australia, Tyskland og New Zealand. Studiene måtte ha blitt publisert på engelsk i fagfellevurderte tidsskrift. Utdanningsnivå ble ikke begrenset og studiene spenner derfor fra barneskole til høyere utdanning og voksenopplæring.
Studiene måtte ta utgangspunkt i omvendt undervisning som inkluderte bruk av videoopptak som forberedelse til matematikktimene. Matematikktimene i klasserommet måtte dessuten være obligatoriske for å sikre at elever og studenter fikk fullt utbytte av omvendt undervisning.
Videre måtte studiene møte følgende inklusjonskriterier:
- a) Studiene måtte sammenligne matematikkprestasjoner i omvendt undervisning med matematikkprestasjoner i tradisjonell undervisning.
- b) Matematikkprestasjonene måtte måles på en objektiv måte ved hjelp av prøver, standardiserte tester eller eksamener. Studier som målte prestasjoner med utgangspunkt i spørreundersøkelser og selvrapportering, ble ekskludert.
- c) Studiene måtte ha gitt nok statistiske data til å beregne effektstørrelser .
- d) Studier som fant signifikante forskjeller mellom elevers kunnskap ved oppstart, måtte bruke statistiske tester for å kontrollere for disse forskjellene i resultatene og fremlegge justerte gjennomsnittsdata.
Resultat
Hvilke undervisningsmetoder ble brukt i og utenfor klasserommet?
Artikkelforfatterne fant store variasjoner i implementeringen av omvendt matematikkundervisning. Alle de inkluderte studiene brukte videoer for å forberede elevene til undervisningen, men noen brukte i tillegg oppgaveark eller stikkord til støtte for læringen/forståelsen. I tillegg til videobasert læring utenfor klasserommet ble noen elever tildelt tekstbasert materiale som for eksempel lærebøker. Noen brukte nettbasert quiz og noen få studier brukte nettbaserte diskusjonsforum.
I det tradisjonelle klasserommet var det mange som startet timen med en quiz om videoen som elevene hadde sett på forhånd. Det var stor bruk av aktiviteter og arbeid i små grupper. Noen satt av tid til individuelt arbeid for og presentasjoner fra enkeltelever. Noen få brukte også deler av tiden i klasserommet til å presentere nytt materiell med tavleundervisning.
Hvordan påvirket omvendt matematikkundervisning elevers prestasjoner?
Artikkelforfatterne fant en statistisk signifikant og positiv effekt på elevenes prestasjoner i matematikk ved bruk av omvendt undervisning sammenlignet med tradisjonell undervisning. Dette gjaldt på tvers av ulike tematikker innen matematikk, som algebra, geometri og statistikk. Der læreren hadde brukt en quiz ved oppstart av hver matematikktime i klasserommet, fant artikkelforfatteren spesielt gode resultater på elevenes prestasjoner.
Hvilken nytte hadde elever og lærere av omvendt undervisning?
Mange elever ga uttrykk for at omvendt undervisning i matematikk resulterte i flere individuelle tilbakemeldinger fra læreren, mer elevassistert læring og mer tid i klasserommet til å anvende ny kunnskap og konsepter gjennom aktiviteter. Elevene fikk langt flere interaksjoner med lærer og medelever, og de brukte mer tid i klasserommet til samarbeid.
Lærere fikk bedre tid til å gi individuelle tilbakemeldinger på elevenes fremgang. De opplevde også at de fikk større spillerom til å legge til rette for undervisningsformer og aktiviteter spesifikt tilpasset sin elevgruppe.
Utenfor klasserommet opplevde elever at det var fordelaktig å ha tilgang til videomateriale. Det hjalp dem med å forberede seg til klasseromsaktiviteter og ga dem mulighet til å se deler av videoene om igjen ved behov til de forstod innholdet. Noen elever så videoene på nytt i for å hjelpe dem med problemløsningsoppgaver eller for å lese til eksamen.
Hvilke utfordringer knyttes til implementering av omvendt matematikkundervisning?
En utfordring i implementeringen av omvendt undervisning i matematikk var elevenes manglende kjennskap til omvendt undervisning. Lærere rapporterte at implementering av omvendt undervisning krevde svært mye arbeid i oppstarten. Forfatterne presiserer at dette er naturlig når man introduserer nye undervisningsmetoder. Noen lærere beskrev arbeidet med omvendt undervisning i matematikk som generelt tidskrevende. Utfordringene knyttet seg til blant annet å finne og lage videomateriell samt til å organisere oppgaver, quiz, gruppearbeid og aktiviteter i klasserommet. Manglende erfaring med omvendt undervisning og begrensede IT-kunnskaper var også en barriere. Noen lærere opplevde at elevene kom uforberedt til timen, noe som resulterte i at læreren måtte bruke mye tid til repetisjon i form av tradisjonell tavleundervisning.
Noen elever synes det var utfordrende å forberede seg til matematikktimene i klasserommet. De var ikke vant til bruk av videoundervisning eller å gjennomføre nettbaserte oppgaver i forkant av matematikktimene og responderte derfor negativt til de nye kravene. Det var også utfordrende for elevene ikke å kunne stille spørsmål umiddelbart når de ikke forstod innholdet i videoene. Det var derfor noen elever som rapporterte at manglende forståelse av videoer reduserte deres opplevelse av læring.
10 prinsipper for implementering av omvendt matematikkundervisning
På bakgrunn av funnene av metasyntesen foreslår artikkelforfatterne følgende 10 prinsipper for implementering av omvendt matematikkundervisning:
- Tilby elevene bred støtte i overgangen fra tradisjonell undervisning til omvendt undervisning.
- Tilby lærerne bred støtte i overgangen fra tradisjonell undervisning til omvendt undervisning.
- For å unngå at elever blir stående fast i forberedelse til skoletimer, bør lærere vurdere å introdusere de mest vanskelige matematiske konseptene i klasserommet. I tillegg bør elever få kontinuerlig støtte i læringsprosessen utenfor klasserommet, gjennom digitale kanaler hvor elevene kan kommunisere og hjelpe hverandre, samt stille spørsmål til læreren.
- Muliggjør effektiv læring ved at læreren selv lager korte videoer.
- Bruk nettbaserte oppgaver med karaktergiving for å motivere elevenes forberedelse til skoletimen.
- Tilpass klasseromsundervisningen basert på resultater fra de overnevnte oppgavene.
- Start skoletimen på en strukturert måte og med utgangspunkt i forberedelsene, for eksempel ved bruk av quiz.
- Legg opp til varierte aktiviteter og virkelighetsnære problemløsningsoppgaver i klasserommet.
- Møt elevenes behov gjennom tilbakemeldinger og tilpasset undervisning.
- Legg til rette for læring gjennom elevsamarbeid ved å organisere små gruppebaserte læringsaktiviteter.
Implikasjoner
Artikkelen gir konkrete tips og forslag til tiltak som lærere kan bruke for å implementere omvendt undervisning i matematikklasserommet. Fordelene ved omvendt undervisning i matematikk berører elevene direkte, i og med at disse fordelene inkluderer flere tilbakemeldinger fra lærer, flere muligheter til samarbeid, samt mer tid til å utforske og forstå vanskelige matematiske konsepter og tematikker. Basert på kunnskapsoversiktens funn kan lærere prøve ut og starte en overgang til omvendt undervisning i matematikk i sine egne klasserom. Forfatterne etterlyser videre studier som prøver ut og evaluerer disse 10 prinsippene.
Kilde:
Lo, Chung Kwan, Hew, Khe Foon, & Chen, Gaowei. (2017). Toward a set of design principles for mathematics flipped classrooms: A synthesis of research in mathematics education. Educational Research Review, 22, 50-73 https://doi.org/10.1016/j.edurev.2017.08.002
